12 Epistemic Logic

One of the uses to which propositional modal logic has been put is to model certain propositional attitudes such as knowledge and belief.

Knowledge

To model knowledge, (⊕Hintikka 1962Hintikka, Kaarlo Jaakko Juhani. 1962. “Knowledge and Belief: An Introduction to the Logic of the Two Notions.”) supplements the language of propositional logic with a family of propositional operators $K_{i}$ for a family of epistemic agents $i \in I$ . A formula of the form $K_{i} φ$ is read: “agent $i$ knows that $φ$ .” Its dual, $\neg K_{i} \neg$ is symbolized: $⟨ K_{i} ⟩$ , is read: “for all agent $i$ knows, $φ$ remains open.”

A relational model $M$ for $L^{K_{i}}$ is a structure $(W, {R_{i} : i \in I}, V)$ , where:

$W$ is a non-empty set of information states or states of the world,
For each $i \in I$ , $R_{i}$ is a binary accessibility relation on $W$ , and
$V$ is a function, which assigns to each propositional variable $p$ a set of states $V (p)$ .

We now define what it is for a formula $φ$ true at a state $s$ in a model $M$ of the form $(W, {R_{i} : i \in I}, V)$ , written $M, s ⊩ φ$ , inductively:

Definition 12.1 (Truth at a State) $\begin{array}{lll} M, s ⊩ p & iff & s \in V (p) \\ M, s ⊩ \neg φ & iff & M, s ⊮ φ \\ M, s ⊩ (φ \to ψ) & iff & M, s ⊮ φ or M, s ⊩ ψ \\ M, s ⊩ K_{i} φ & iff & for every u \in W s.t. R_{i} s u, M, u ⊩ φ \end{array}$ We define $⟨ K_{i} ⟩$ as the dual of $K_{i}$ , that is, $\neg K_{i} \neg$ , which means: $\begin{array}{lll} M, s ⊩ ⟨ K_{i} ⟩ φ & iff & for some u \in W s.t. R_{i} s u, M, u ⊩ φ \end{array}$

We are now in a position to define truth in a model of epistemic logic.

Definition 12.2 (Truth in a Model) A formula $φ$ is true in a model $M$ of the form $(W, {R_{i} : i \in I}, V)$ , written $M ⊩ φ$ , if, and only if, for every $s \in W$ , $M, s ⊩ φ$ .

Knowledge provides the ability to locate the actual world in the space of epistemic live options, and, in particular, to exclude certain states of the world as candidates for actuality. One information state $v$ is i-accessible from $u$ iff $v$ remains an epistemic live option for the agent $i$ in state $u$ , one the agent $i$ is not able to exclude as a candidate for actuality. That is, nothing the agent $i$ knows enables $i$ to distinguish $v$ from the actual world.

These decisions are not inconsequential. For it follows that agents know all logical truths and that they know what follows from what they know. That is the framework vindicates a rule of necessitation and all substitution instances of axiom K: $\begin{matrix} (N) & φ / K_{i} φ \end{matrix}$

$\begin{matrix} (K) & K_{i} (p \to q) \to (K_{i} p \to K_{i} q) \end{matrix}$ This involves a modicum of idealization: ordinary knowledge is not closed under logical consequence, and it is not all that plausible to think agents ordinarily know all logical truths.

One way to cope with this observation is to let $K_{i}$ model not ordinary knowledge but rather knowledge by an idealized agent equipped with unlimited logical capabilities. Alternatively, one may instead take $K_{i}$ to model implicit knowledge, which is what follows from knowledge we may reasonably attribute to ordinary agents even if it is not explicitly known by them.

The next step is to consider the epistemic interpretation of different modal axioms and to ask whether or not they are candidates for the logic of knowledge.

$\begin{matrix} (T) & K_{i} p \to p \end{matrix}$

What is known is the case.

The principle that knowledge implies truth is virtually universally accepted, and a firm candidate for the logic of knowledge.

From a semantic point of view, $T$ requires $i$ -accessibility relations to be reflexive: a state itself is a live epistemic option for an agent.

$\begin{matrix} (4) & K_{i} p \to K_{i} K_{i} p \end{matrix}$ What is known is known to be known.

This is the principle commonly known as the $K K$ -principle. It encodes the view that knowledge is transparent to the agent: if you know something, then you know that you know. Presumably, the thought is that agents with unlimited introspection capabilities ought to be able to recognize their own knowledge: agents should be able to introspectively attend to their reasons for belief, which should be conclusive in cases of knowledge and not defeasible by new information.

From a semantic point of view, $4$ requires the $i$ -accessibility relations to be transitive: if a state $t$ is an epistemic live option for $i$ at $v$ , and $v$ is a live option for $i$ at $u$ , then $t$ is a live option for $i$ at $u$ .

(⊕Hintikka 1962Hintikka, Kaarlo Jaakko Juhani. 1962. “Knowledge and Belief: An Introduction to the Logic of the Two Notions.”) adopted axioms $T$ and $4$ and identified $S 4$ as a candidate logic for knowledge. His reasons for that is that he regarded axioms $B$ and $5$ as implausible epistemic principles.

$\begin{matrix} (B) & p \to K_{i} ⟨ K_{i} ⟩ p \end{matrix}$ What is the case is known to be open.

This means that we could come to know that something that is the case is open merely by reflection on that fact, which seems implausible. This is clearer when we look at the contrapositive of the principle: $\begin{matrix} (B_{◊}) & ⟨ K_{i} ⟩ K_{i} p \to p \end{matrix}$ It is not implausible to think an agent may take themselves to know something that is in fact not the case. That would be a case in which knowledge that they know something would not be ruled out despite the fact that what is taken to be known is not the case. But that again is supposed to be ruled out by $B_{◊}$ .

The semantic counterpart of these observations is that we should not automatically rule out failures of symmetry for $i$ -accessibility relations: from the fact that $v$ is an epistemic live option for the agent at $u$ , we cannot conclude that $u$ is an epistemic live option for the agent at $v$ .

To the extent to which $K T B 4$ is equivalent to $K T 5$ or $S 5$ , the above considerations extend to axiom $5$ , which in the presence of $T$ would give us $B$ .

$\begin{matrix} (5) & ⟨ K_{i} ⟩ p \to K_{i} ⟨ K_{i} ⟩ p \end{matrix}$ What is open is known to be open.

There are cases in which agents take themselves to know something that is not in fact the case. Because knowledge entails truth, it would be false in that case that the agents know. But the agents might not have access to that information: it may be open to them that they know despite the fact that they do not know that it is open to them to know. One way to put it is that $5$ would require agents to be immune to error of the sort described, which is again quite implausible.

We now illustrate further uses of epistemic logic by means of a well-known example.

Information Flow

The insight behind the possible worlds semantics for epistemic logic is that agents locate themselves in the space of epistemic live options by excluding states of the world as live options in light of new information. The Muddy Children puzzle illustrates the dynamic aspect of this update mechanism:

Example 12.1 (Muddy Children) Three children $a$ , $b$ , and $c$ have been playing outside when they are called back inside by their guardian. Two of them, say $a$ and $c$ , have mud on their forehead, but none of them is able to see their own forehead. Each child, however, can see which of the other children are muddy. Once inside, the guardian asserts:

At least one of you is muddy.

followed by an initial request:

If you know you are muddy, please step forward.

None of the children will presumably step forward after the first request. Each child will see other children with mud in their foreheads, but none of them will know whether they themselves are muddy.

Matters change when she repeats the same request for a second time:

If you know you are muddy, please step forward.

After the second request, the two muddy children will step forward while the third stays behind. For they now know that they are muddy.

The example raises a number of questions:

Did the children learn anything new after the announcement that one of them was muddy?
What changed between the initial request when no one stepped forward and the later one when two muddy children did?
How did the two muddy children come to know that they had mud in their foreheads?

Here is a diagrammatic representation of the situation before the initial announcement.

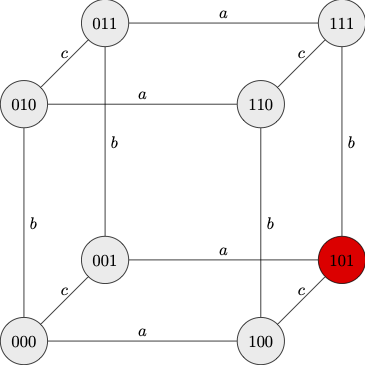Before Announcement A

We represent the relevant states of information with respect to the question at hand by ordered triples of digits, which encode the state of each children in that order. Thus for example:

$101$ encodes the actual state of the world on which $a$ is muddy, $b$ is not muddy, and $c$ is muddy.
$111$ encodes an epistemic live option for $b$ (though not for $a$ or $c$ ) on which all three children are muddy.
$001$ encodes an epistemic live option for $a$ (though not for $b$ or $c$ ) on which only $c$ is muddy.

The eight nodes correspond to eight states, which consist of different distributions of mud across the children. The nodes are connected by different accessibility relations, which correspond to each child as an epistemic agent. We assume that each relation is reflexive and symmetric: when an edge labeled $a$ , for example, connects two nodes, the two states are indistinguishable as far as $a$ is concerned.

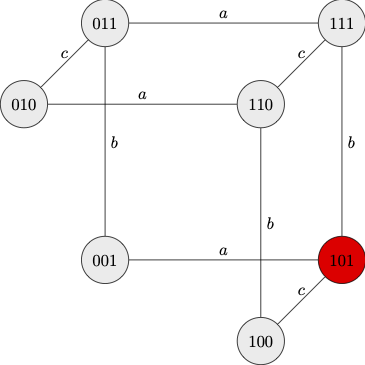The effect of the announcement $A$ is to let the children exclude $000$ as a live epistemic option.

After Announcement A

While announcement $A$ excludes $000$ as actuality, none of the children regarded $000$ as an epistemic live option. That is because each children is able to see mud in the forehead of at least one child.

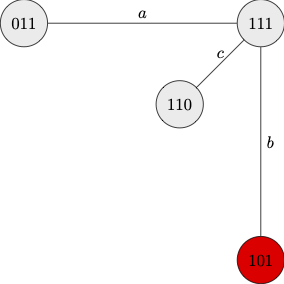The children learn valuable information from the fact that no one steps forward after request $B$ is made. This is because the children now learn that none of the other two children know that they are muddy. This suffices to rule out states at which there is exactly one muddy child.

After Request B

After request B, $a$ and $c$ will simultaneously step forward since they find no epistemically open alternative at which they are not muddy. On the other hand, $b$ will stay back because she cannot tell which of $101$ or $111$ are actual. That is, $b$ stays back because $b$ cannot rule out that she is not is muddy.

That allows the children to eliminate all epistemic alternatives to $101$ . So, the epistemic situation after the second request is that the children know exactly who is muddy and who is not muddy.

After Request C

Nothing changes when we complicate the situation. If, for example, seven out of ten children happened to be muddy, then no one would step forward until after the guardian makes the seventh request at which point exactly those seven children would simultaneously step forward. More generally, given $n$ muddy children, $n$ rounds of

Common Knowledge

What do the children learn after the first announcement? Notice that they all know that at least one child is muddy even prior to the announcement. We may use $E φ$ as an abbreviation for the conjunction: $\underset{i \in I}{⋀} K_{i} φ,$ which is read: “it is generally known that $φ$ ’’. General knowledge is not sufficient for common knowledge. A group has common knowledge that $φ$ if they all know that $φ$ , they all know that they all know that $φ$ , they all know that they all know that they all know that $φ$ , etc.

Example 12.2 Let us revisit the initial model for the Muddy Children Puzzle and let $p_{1}$ , $p_{2}$ , and $p_{3}$ be true at exactly states at which each of $a$ , $b$ , and $c$ , respectively, are muddy, then we may express the fact that at least one child is muddy by means of the disjunction $p_{1} \lor p_{2} \lor p_{3}$ . Notice that that formula is true when evaluated at state $101$ : $M, 101 ⊩ E (p_{1} \lor p_{2} \lor p_{3}) .$

That is because: $M, 101 ⊩ K_{a} (p_{1} \lor p_{2} \lor p_{3}) \land K_{b} (p_{1} \lor p_{2} \lor p_{3}) \land K_{c} (p_{1} \lor p_{2} \lor p_{3}) .$ But although it is generally known that at least one child is muddy, it is not common knowledge that at least one child is muddy.

Common knowledge plays a crucial role in social interaction. When we drive, for example, we rely on the fact that it is common knowledge that a red light requires drivers to stop. It is not sufficient for a pedestrian to know that, but it is important to know that drivers know that and for them to know that everyone knows that, etc.

How should we incorporate common knowledge in the language of epistemic logic? There is no hope for an explicit definition of common knowledge in terms of knowledge, for that would presumably require an infinite conjunction, which is not available in the language. We will instead expand the language of epistemic logic with a common knowledge operator, $C φ$ , reqd: “it is common knowledge that $φ$ .

Once we do this, we must explain how to evaluate a formula of the form $C φ$ at a state $s$ of a model $M$ of the form $(W, {R_{i} : i \in I}, V)$ . To that purpose, we will expand the definition of truth at a state with a clause for the newly added common knowledge operator.

a state $t$ is reachable from $s$ in one step, in symbols, $s R^{1} t$ , iff $s R_{i} t$ for some $i \in I$ . In the case at hand, one state is reachable from another in one step if it is $a$ -accessible from the other or it is $b$ -accessible from the other or, finally, it is $c$ -accessible from the other.
a state $t$ is reachable from $s$ in $n + 1$ steps, in symbols, $s R^{n + 1} t$ , iff for some step $u$ , $s R^{n} u$ and $u R_{i} t$ for some $i \in I$ .

Example 12.3 For purposes of illustration, notice that in the initial model for the Muddy Children Puzzle $000$ is reachable from $101$ in two steps: $101 R_{c} 100 and 100 R_{a} 000$ $101 R_{a} 001 and 001 R_{c} 000$

That is, there are two-step paths one may take from $101$ to $000$ .

Finally,

a state $t$ is reachable from $s$ in a finite number of steps, in symbols $R^{⋆}$ , iff there is some $n$ such that $t$ is reachable from $s$ in $n$ steps.

Here is the clause for $C φ$ in the definition of truth at a state: $\begin{array}{lll} M, s ⊩ C φ & iff & for every u \in W s.t. R^{⋆} s u, M, u ⊩ φ \end{array}$

In other words, $C φ$ is true at a state $s$ iff $φ$ is true at every state $t$ reachable from $s$ in a finite number of steps.

Example 12.4 (Common Knowledge and Muddy Children) Let us revisit the model for the Muddy Children Puzzle prior to the first announcement:

Before Announcement A

When we apply the definition of truth at a state to the case at hand, we find: $M, 101 ⊮ C (p_{1} \lor p_{2} \lor p_{3}) .$ The reason is that the state $000$ , which falsifies the disjunction, is reachable from $101$ in two steps.

The situation changes once the children eliminate that option after the announcement. One of the effects of the announcement in the Muddy Children Puzzle is to make it common knowledge that at least one child is muddy: it is not just that all children know that at least one child is muddy, all children now know that all children know, and all children know that all children know that they know that, etc.

After Announcement A

If we use $M^{'}$ to refer to the model that results, we find $M^{'}, 101 ⊩ C (p_{1} \lor p_{2} \lor p_{3}) .$

This is because the disjunction is true at every state reachable from $101$ in the new model.

After the first request is made without any children stepping forward, the children are able to rule out as epistemic alternatives states in which only one child is muddy.

After Request B

At this point, the fact that two children are muddy now becomes common knowledge, since only states where two children are muddy are reachable from the state of evaluation in a finite number of steps.

The actual distribution of mud becomes common knowledge after the two children step forward after the thrid request. That is because they are all left with a single epistemic live option:

After Request C

The accessibility relation for common knowledge, $R^{⋆}$ , will of course be reflexive and transitive. It will be transitive by definition, but it will inherit reflexivity from the reflexivity of each of the $i$ -accessibility relations. Whether the relation will in addition be symmetric or euclidean will crucially depend on the structure of the individual $i$ -accessibility relations.

One axiomatization of the logic of common knowledge employs an an axiom and a rule of inference: $\begin{matrix} (Fixed Point) & C p \to E (p \land C p) \end{matrix}$ $\begin{matrix} (Induction) & φ \to E (ψ \land φ) / φ \to C ψ \end{matrix}$

The fixed point axiom regards common knowledge as a fixed point of the function that maps a formula $φ$ to $K_{i} (φ \land C φ)$ .

The rule of inference is called an induction rule because the antecedent provides the crucial ingredient for an inductive argument for all instances of the schema: $φ \to E^{n} (ψ \land φ),$ which guarantees the conditional $φ \to C ψ .$ For suppose the conditional $φ \to E (ψ \land φ)$ is valid. Then if $v a r p h i$ is true at $s$ , $E (ψ \land φ)$ is true at $s$ , which means that if $t$ is reachable from $s$ in one step, then $φ$ is true at $t$ . So, $E (ψ \land φ)$ is true at $t$ . If $u$ is now reachable from $t$ in one step, then $E (ψ \land φ)$ will be true at $t$ , etc.

We are in a position to prove some theorems of the logic of common knowledge.

Proposition 12.1 $⊢ C p \to E C p$

Proof. This is a simple consequence of the Fixed Point axiom: $\begin{array}{lllll} 1 & C p \to E (p \land C p) & Fixed Point \\ 2 & E (p \land C p) \to (E p \land E C p) & K 1 \\ 3 & C p \to E C p & PL 1, 2 \end{array}$

Proposition 12.2 $⊢ C p \to C C p$

Proof. This is a simple consequence of the rule of inference for common knowledge. $\begin{array}{lllll} 1 & C p \to E C p & Prop. 9.1 \\ 2 & C p \to (C p \land C p) & PL \\ 3 & E C p \to E (C p \land C p) & PL \\ 4 & C p \to E (C p \land C p) & PL 1, 3 \\ 5 & C p \to C C p & RC [C p / φ, C p / ψ] 4 \end{array}$

Belief

Modal logic provides a formal framework for a study of the interplay between knowledge and belief. (⊕R. Stalnaker 2006Stalnaker, Robert. 2006. “On Logics of Knowledge and Belief.” Philosophical Studies: An International Journal for Philosophy in the Analytic Tradition 128 (1): 169–99.) proposes to supplement the language of epistemic logic with a family of further propositional operators $B_{i}$ for a family of epistemic agents $i \in I$ . A formula of the form $B_{i} φ$ is read: “agent $i$ believes that $φ$ .” Its dual, $\neg B_{i} \neg$ is symbolized: $⟨ B_{i} ⟩$ , is read: “for all agent $i$ believes, $φ$ remains open.”

We supplement the relational models of epistemic logic with a family of accessibility relations ${S_{i} : i \in I}$ for belief, and we extend the inductive definition of truth at a state in a model $M$ of the form $(W, {R_{i} : i \in I}, {S_{i} : i \in I}, V)$ , written $M, s ⊩ φ$ , with a further clause for formulas of the form $B_{i} φ$ :

Definition 12.3 (Truth at a State) $\begin{array}{lll} M, s ⊩ B_{i} φ & iff & for every u \in W s.t. S_{i} s u, M, u ⊩ φ \end{array}$ There is a derived rule for $⟨ B_{i} ⟩ φ$ : $\begin{array}{lll} M, s ⊩ ⟨ K_{i} ⟩ φ & iff & for some u \in W s.t. S_{i} s u, M, u ⊩ φ \end{array}$

Belief, like knowledge, aims to locate the actual world in the space of doxastic live options, and, in particular, to exclude certain states of the world as candidates for actuality. One belief state $v$ is i-accessible from $u$ iff $v$ remains an doxastic live option for the agent $i$ in state $u$ , one the agent $i$ is not able to exclude as a candidate for actuality. That is, nothing the agent $i$ knows enables $i$ to distinguish $v$ from the actual world.

Axioms for Knowledge and Belief

The logic of knowledge and belief includes axioms for the interaction between the two propositional attitudes. (⊕R. Stalnaker 2006Stalnaker, Robert. 2006. “On Logics of Knowledge and Belief.” Philosophical Studies: An International Journal for Philosophy in the Analytic Tradition 128 (1): 169–99.) offers a concrete proposal, which begins with the factivity of knowlegde: $\begin{matrix} (T) & K_{i} p \to p \end{matrix}$ What is known is the case

We observed that this amounts to the requirement that the $i$ -accessibility relations for knowledge must be reflexive.

Factivity is not at all plausible when it comes to belief; we often believe what is not the case. There is, however, a weaker constraint on belief we should consider, namely, that an agent never believes a proposition and its negation. Since $⟨ B_{i} ⟩$ abbreviates: $\neg B_{i} \neg$ , the consistency requirement on belief amounts to the adoption of axiom $D$ for belief: $\begin{matrix} (D) & B_{i} p \to ⟨ B_{i} ⟩ p \end{matrix}$ If one believes something, one does not believe its negation.

That in turn requires the $i$ -accessibility relations for belief to be serial: for each doxastic state, there is a doxastic alternative for each $i$ -agent.

None of these axioms constrains the interaction between knowledge and belief, but it seems that a minimal constraint on knowledge is that belief is necessary for knowledge. We know that belief is not sufficient for knowledge and the point of the classic analysis of knowledge in terms of justified true belief is to find further necessary and sufficient conditions for knowledge. The next axiom encodes the principle that belief is a necessary condition for knowledge.

$\begin{matrix} (KB) & K_{i} p \to B_{i} p \end{matrix}$ One believes what one knows.

This principle requires every doxastic alternative to count as an epistemic alternative to the state of evaluation $s$ : if a state $t$ is doxastically $i$ -accessible from $s$ , then $t$ is epistemically $i$ -accessible from $s$ . In other words, if $S_{i} s t$ , then $R_{i} s t$ . This is because a proposition is true in all epistemic live options only if it is true in all doxastic live options.

Two more axioms encode the assumption that agents have epistemic introspective access to their doxastic states:

$\begin{matrix} (Positive Introspection) & B_{i} p \to K_{i} B_{i} p \end{matrix}$

One knows that one believes what one believes

Positive Introspection says that an agent believes something only if they know that they believe it. On the other hand, Negative Introspection tells us that something is doxastically open for an agent only if they know that it is doxastically open.

$\begin{matrix} (Negative Introspection) & ⟨ B_{i} ⟩ p \to K_{i} ⟨ B_{i} ⟩ p \end{matrix}$ One knows that what is doxastically open is doxastically open

Since knowledge entails belief, we derive weaker forms of introspection for belief as immediate consequences: $B_{i} p \to B_{i} B_{i} p ⟨ B_{i} ⟩ p \to B_{i} ⟨ B_{i} ⟩ p$ (⊕R. Stalnaker 2006Stalnaker, Robert. 2006. “On Logics of Knowledge and Belief.” Philosophical Studies: An International Journal for Philosophy in the Analytic Tradition 128 (1): 169–99.) observes that these axioms suffice to ensure that the pure logic of belief is $K D 45$ , which is complete with respect to the class of serial, transitive, and euclidean frames.

The choice of axioms is not inconsequential for the pure logic of knowledge, which turns out to extend $S 4$ to include all substitution instances of the axiom:

$\begin{matrix} (G) & ⟨ K_{i} ⟩ K_{i} p \to K_{i} ⟨ K_{i} ⟩ p \end{matrix}$ If it is epistemically open that one knows that $p$ , then one knows that $p$ is epistemically open.

That will, in turn, require the relations of epistemic $i$ -accessibility to be convergent, where a binary relation $R_{i}$ on $W$ is convergent iff

for all $x, y, z \in W$ , if $R_{i} x y$ and $R_{i} x z$ , then there is some $t \in W$ such that $R y t$ $R z t$ .

The modal logic $S 4.2$ is $K T 4 G$ , which is sound and complete with respect to the class of reflexive, transitive, and convergent frames.

Proposition 12.3 $⊢ ⟨ K_{i} ⟩ K_{i} p \to K_{i} ⟨ K_{i} ⟩ p$

Proof. Here is a derivation of $G$ from $N I$ , $K B$ , and $C B$ : $\begin{array}{lllll} 1 & ⟨ B_{i} ⟩ p \to K_{i} ⟨ B_{i} ⟩ p & Negative Introspection \\ 2 & ⟨ B_{i} ⟩ p \to ⟨ K_{i} ⟩ p & {Knowledge requires Belief}_{◊} \\ 3 & K_{i} ⟨ B_{i} ⟩ p \to K_{i} ⟨ K_{i} ⟩ p & RK 2 \\ 4 & ⟨ B_{i} ⟩ p \to K_{i} ⟨ K_{i} ⟩ p & PL 1, 3 \\ 5 & ⟨ K_{i} ⟩ K_{i} p \to B_{i} p & Dual of line 4 \\ 6 & B_{i} p \to ⟨ B_{i} ⟩ p & Consistency \\ 7 & ⟨ K_{i} ⟩ K_{i} p \to K_{i} ⟨ K_{i} ⟩ p & PL 5, 6, 4 \end{array}$

There is one final constraint to consider, which concerns the very nature of belief. (⊕R. Stalnaker 2006Stalnaker, Robert. 2006. “On Logics of Knowledge and Belief.” Philosophical Studies: An International Journal for Philosophy in the Analytic Tradition 128 (1): 169–99.) proposes to conceive of belief as a propositionally attitude which is internally indistinguishable from knowledge. To believe something is to believe you know it. That is if you hesitate when you consider whether you know something, then you do not genuinely believe it. This is the axiom Stalnaker calls Subjective Certainty:

$\begin{matrix} (SC) & B_{i} p \to B_{i} K_{i} p \end{matrix}$ You only believe you have hands if you believe you know you have hands; if consideration of a skeptical scenario somehow drives you to not believe that you know that you have hands, then you no longer genuinely believe that you have hands.

This axiom turns out to have an important ramification for the logic of belief and knowledge. For given $G$ above, we may reverse the conditional in line 5 of the proof of $G$ above. That is, we may prove that belief is sufficient for knowledge to be epistemically open.

Proposition 12.4 $⊢ B_{i} p \to ⟨ K_{i} ⟩ K_{i} p$

Proof. Here is a derivation $\begin{array}{lllll} 1 & B_{i} p \to B_{i} K_{i} p & Subjective Certainty \\ 2 & B_{i} K_{i} p \to ⟨ B_{i} ⟩ K_{i} p & Consistency \\ 3 & ⟨ B_{i} ⟩ K_{i} p \to ⟨ K_{i} ⟩ K_{i} p & {Knowledge entails Belief}_{◊} \\ 4 & B_{i} p \to ⟨ K_{i} ⟩ K_{i} p & PL 1, 2, 3 \end{array}$

When combined, we find that the axioms of knowledge and belief enforce an equivalence between belief and a species of ignorance: you believe if, and only if, you do not not know that you know.

Proposition 12.5 $⊢ B_{i} p \leftrightarrow ⟨ K_{i} ⟩ K_{i} p$

Proof. One direction is line 5 in the derivation of $G$ , whereas the other is the conditional we proved above.

We have derived the biconditional in the logic of knowledge and belief, but a different course of action would have been to remain in the language of epistemic logic and introduce a belief operator as a defined operator: $B_{i} φ := ⟨ K_{i} ⟩ K_{i} φ$ Against the background of $S 4.2$ as a logic of knowledge, we would be in a position to prove as theorems the axioms that correspond to $K D 45$ as a pure logic of belief.