1 Introduction

Propositional logic classifies propositions into main categories: true and false. Alethic modal logic makes distinctions between different modes in which a proposition may be true or false. The formal framework of modal logic expands the language of propositional logic with a sentential operator, $◻$ , for one of those modes, i.e., necessity, and a dual operator, $◊$ , for another, i.e., possibility.

Other interpretations of the formalism take the sentential operators in question to provide a different qualification to the proposition expressed by the sentence in question.

$\begin{array}{lll} ◻ & ◊ \\ alethic & necessarily & possibly \\ temporal & always & sometimes \\ epistemic & known & for all we know \\ deontic & required & permitted \end{array}$ These distinctions play a crucial role in philosophy.

Example 1.1 (Modal Ontological Argument) Given the nature of numbers, necessarily, if they exist at all, then they are necessary beings. It is at least possible that numbers exist. So, it is possible that numbers are necessary beings. It follows that there are numbers.

In premise-conclusion form, the argument becomes:

Necessarily, if numbers exist, then they exist necessarily.
It is possible that numbers exist.
It is possible that numbers exist necessarily.
Numbers exist.

The argument is propositionally invalid, but it nevertheless retains a measure of plausibility. If we let $p$ stand for the proposition that numbers exist, we may formalize the argument in the framework of propositional modal logic:

$\begin{array}{lllll} 1 & ◻ (p \to ◻ p) \\ 2 & ◊ p \\ 3 & ◊ ◻ p \\ 4 & p \end{array}$ The question now is how to assess its validity. That is, does the conclusion of the argument follow from its premises? We will not be in a position to answer these questions until we explain how to interpret the formalism.

Example 1.2 (Aristotle's Sea Battle) If there is a sea battle tomorrow, Aristotle reasons, then it was already the case in the past that there would be a sea battle tomorrow. But that could have not been otherwise, since the past is closed. However, if it is necessary that it was the case that there would be a sea battle tomorrow, then it should still be necessary that there will be a sea battle tomorrow. So, if there is a sea battle tomorrow, then it is already necessary that there will be one.

Aristotle appears to take as a point of departure the thought that whatever we think of the future, the past is closed. To the extent to which we cannot change the past, whatever was the case must have been the case. Aristotle’s argument is meant to target the alleged contrast between past and future: it is incoherent to suppose that the future is open if the past is already closed.

If there will be a sea battle tomorrow, then it was the case in the past that there would be a sea battle tomorrow.
If it was the case in the past that there would be a sea battle tomorrow, then it is necessary that it was the case in the past that there would be a sea battle tomorrow.
If it is necessary that it was the case in the past that there would be a sea battle tomorrow, then it is necessary that there will be a sea battle tomorrow.
So, if there will be a sea battle tomorrow, then it is necessary that there will be a sea battle tomorrow.

The argument relies now on the interaction between different modalities, two temporal ones such as $F$ for ‘it will once be the case that’ and $W$ for ‘it was once the case that’, and an alethic operator $◻$ for ‘it is necessary that’.

$\begin{array}{lllll} 1 & F p \to W F p \\ 2 & W F p \to ◻ W F p \\ 3 & ◻ W F p \to ◻ F p \\ 4 & F p \to ◻ F p \end{array}$

The question of validity is more complicated than in the earlier example as this argument takes place in a multi-modal language with temporal and alethic modal operators.

Let us return to the question of how to interpret the formalism of propositional modal logic. There is, in particular, an important contrast to be drawn between propositional logic and propositional modal logic.

We are able to use truth tables to interpret the language of propositional logic because propositional connectives are truth-functional, e.g., the truth value of a conjunction is a function of the truth values of its conjuncts. The strategy does not seem to be available in the case of modal logic, since the modal operator $◻$ is not truth-functional:

$\begin{array}{cc} φ & ◻ φ \\ T & ? \\ F & F \end{array}$

When $φ$ is false, $◻ φ$ will of course be false. But the truth of $φ$ leaves open whether $◻ φ$ is true or false, e.g., $◻ φ$ will be true when $φ$ is a tautology but false when $φ$ is interpreted to make a contingent statement.

One may attempt to overcome this limitation with the help of a more fine-grained distinction between necessary and contingent truths, on the one hand, and necessary and contingent falsehoods, on the other. We may even reserve the letters $t$ and $T$ for contingent and necessary truths respectively, and we may similarly use $f$ and $F$ for contingent and necessary falsehoods respectively. This appears to suggests a truth table for each negation and $◻$ :

$\begin{array}{ccc} φ & \neg φ & ◻ φ \\ T & F & T \\ t & f & F \\ F & T & F \\ f & t & F \end{array}$ Even if there is a measure of plausibility to these tables, the problem arises when we attempt to generalize the framework to cover other propositional connectives such as the material conditional. Once we opt for the more fine-grained distinction between necessary and contingent truths and falsehoods, the truth value of the conditional ceases to be a function of the truth values of antecedent and consequent.

$\begin{array}{ccccc} \to & T & t & F & f \\ T & T & t & F & f \\ t & T & ? & F & f \\ F & T & T & T & T \\ f & T & t & t & ? \end{array}$

When $φ$ and $ψ$ are contingently true, $φ \to ψ$ may be necessarily true, e.g., $p \to p$ if $p$ is contingently true, or merely contingently true, e.g., $p \to q$ for suitable choices of contingent propositions $p$ and $q$ . Likewise, when $φ$ and $ψ$ are contingently false, the conditional may be necessarily or contingently true.

We must look elsewhere for an interpretation of the formalism of propositional modal logic. One key observation at this point is that propositions differ not just with respect to whether they are true or false, they may differ with respect to the circumstances under which they are true or false. The propositions expressed by the statements ‘Los Angeles has over three million inhabitants’ and ‘Kilimanjaro rises to 5,895 meters’ are both true but there are possible circumstances under which one is true and the other is false.

We may think of possible worlds as complete specifications of a way the world might be, and we may ask whether a sentence is true at a possible world. That is, we may ask whether the possible world in question specifies circumstances under which the sentence is in fact true.

Once we take on board the thought that a sentence may be true when evaluated with respect to one possible world but not when evaluated with respect to another, we may ask what is for a possible world to be possible relative to another. The proposition that I’m a philosopher is true given how the world is, but there are possible circumstances under which I’m an engineer. We codify that as the thought that a world at which I’m an engineer is possible with respect to the world of evaluation. We will call a possible world is accessible from another world if the former is possible with respect to the latter.

We now have the basic ingredients for a possible world semantics for propositional modal logic. More formally, a model for the framework will consist of a collection of possible worlds $W$ , an accessibility relation $R$ on the collection $W$ , and a valuation function, which specifies which propositions are true at what possible worlds.

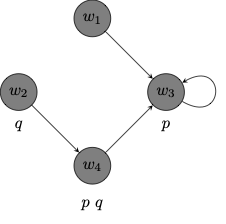
Example 1.3 (A Possible Worlds Model) Here is a depiction of a possible worlds model, which consists of a set $W$ of four worlds and a binary relation $R$ on $W$ . The model verifies $p$ at $w_{3}$ and $w_{4}$ , and it verifies $q$ at $w_{2}$ and $w_{4}$ .

A negation $\neg φ$ is true at a world $w$ if, and only if $φ$ is false at that world.
A material conditional $φ \to ψ$ is true at a world $w$ just in case $φ$ is false at $w$ or $ψ$ is true at $w$ .
A formula $◻ φ$ is true at a world $w$ if, and only if, $φ$ is true at every world $u$ to which $w$ is related.
A formula $◊ φ$ is true at a world $w$ if, and only if, $φ$ is true at some world $u$ to which $w$ is related.

Consider the premises and conclusion of the modal formalization of the argument with which we started:

$p \to ◻ p$ is true in every world in the model.

Therefore,

$◻ (p \to ◻ p)$ is true at every world in the model.
$◊ p$ is true at every world in the model.
$◻ p$ is true at every world in the model.
$◊ ◻ p$ is true at every world in the model.
$p$ is true at $w_{3}$ and $w_{4}$ but not at either $w_{1}$ or $w_{2}$ .

It follows that $w_{1}$ and $w_{2}$ are each a world that verifies every premise of the argument but not its conclusion.

It will turn out that the validity of the argument for the existence of numbers turns on the structure of the accessibility relation. That is, the argument will be valid when we restrict attention to models in which the accessibility relation is either symmetric or models in which the accessibility relation is reflexive and euclidean.11 Please do not worry if any of those terms are new to you. Much of what we will do before we formally introduce the language of propositional modal logic is to cover some preliminaries, which will include some discussion of the structure of binary relations.