17 Semantics

Constant Domain Models

We have provided a syntactic characterization of the simplest quantified modal logic, but we should now explain how to interpret the language in order to validate its axioms.

Definition 17.1 (Constant Domain Model) We define a constant domain model to be structure $M$ of the form $(W, R, D, I)$ , where:

$W$ is a non-empty set of worlds.
$R$ is a binary accessibility relation on $W$
$D$ is a non-empty set of individuals, and
$I$ is a function from worlds $w$ into interpretations $I_{w}$ , which map each $n$ -place predicate $P^{n}$ into an $n$ -place relation over $D$ .

Definition 17.2 (Variable Assignment for a Model) A variable assignment $α$ for a model $M$ is a function from individual variables into members of $D$ .

We now define what is for a formula $φ$ to be true at a world $w$ in a model $M$ relative to an assignment $α$ . In what follows, $α [x / d]$ is an assignment just like $α$ except perhaps for assigning $d$ to the variable $x$ .

Definition 17.3 (Truth at a World Relative to an Assignment) We use a recursive definition: $\begin{array}{lll} M, w, α ⊩ P^{n} v_{1} \dots v_{n} & if, and only if, & ⟨ α (v_{1}), \dots, α (v_{n}) ⟩ \in I_{w} (P^{n}) \\ M, w, α ⊩ v_{1} = v_{2} & if, and only if, & α (v_{1}) = α (v_{2}) \\ M, w, α ⊩ \neg φ & if, and only if, & M, w, α ⊮ φ \\ M, w, α ⊩ (φ \to ψ) & if, and only if, & M, w, α ⊮ φ or M, w, α ⊩ ψ \\ M, w, α ⊩ \forall x φ & if, and only if, & M, w, α [x / d] ⊩ φ for every d \in D \\ M, w, α ⊩ ◻ φ & if, and only if, & M, u, α ⊩ φ for every u \in W such that R w u \end{array}$

We now define truth at a world in a model and truth in. a model respectively:

Definition 17.4 (Truth at a World) A formula $φ$ is true at a world $w$ in a model $M$ , in symbols $M, w ⊩ φ$ , if, and only if, for all assignments $α$ for $M$ , $M, w, α ⊩ φ$

Definition 17.5 (Truth in a Model) A formula $φ$ is true in a model $M$ , in symbols, $M ⊩ φ$ , if, and only. if, for all $w \in W$ , $M, w ⊩ φ$ .

Definition 17.6 (Validity in a Class of Models) A formula $φ$ is valid with respect to a class $C$ . of constant domain models, in symbols $⊨_{C} φ$ , if, and only if, for every constant domain model $M \in C$ , $M ⊩ φ$ .

It will be helpful to provide some illustration. We explain first how to justify the fact that a certain formula is not valid with respect to the class of reflexive and euclidean models.

Example 17.1 $⊭_{refl and eucl} \exists x \neg ◻ F x \to ◊ \forall x \neg F x$

Consider a constant domain model $M$ of the form $(W, R, D, I)$ , where:

$W = {w_{1}, w_{2}}$
$R = {(w_{1}, w_{1}), (w_{1}, w_{2}), (w_{2}, w_{1}), (w_{2}, w_{2})}$
$D = {a, b}$
$I_{w_{1}} (F) = {a}$

$I_{w_{2}} (F) = {b}$

Here is a diagram for the model:

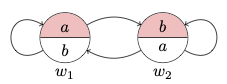
Now:

$M, w_{1} ⊩ \exists x \neg ◻ F x$ because $M, w_{1}, α [b / x] ⊩ \neg ◻ F x$
$M, w_{1} ⊮ ◊ \forall x \neg F x$ because $M, w_{1} ⊩ \forall x \neg F x$ and $R w_{1} w_{1}$ .

Example 17.2 $⊭_{refl and eucl} (◻ \exists x F x \lor \forall x ◊ G x) \to ◊ \exists x (F x \land G x)$

Consider a constant domain model $M$ of the form $(W, R, D, I)$ , where:

$W = {w_{1}, w_{2}}$
$R = {(w_{1}, w_{1}), (w_{1}, w_{2}), (w_{2}, w_{1}), (w_{2}, w_{2})}$
$D = {a, b}$
$I_{w_{1}} (F) = {a}$ , $I_{w_{1}} (G) = {b}$

$I_{w_{2}} (F) = {b}$ , $I_{w_{2}} (G) = {a}$

Here is a diagram for the model:

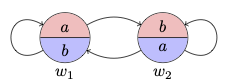
Now:

$M, w_{1} ⊩ ◻ \exists x F x$ since $M, w_{1} ⊩ \exists x F x$ and $M, w_{2} ⊩ \exists x F x$
$M, w_{1} ⊮ ◊ \exists x (F x \land G x)$ since $M, w_{1} ⊮ \exists x (F x \land G x)$ and $M, w_{2} ⊮ \exists s (F x \land G x)$

Example 17.3 $⊭_{refl and eucl} \forall x (◻ F x \lor ◻ \neg F x) \lor \forall x (◊ F x \land ◊ \neg F x)$

Consider a constant domain model $M$ of the form $(W, R, D, I)$ , where:

$W = {w_{1}, w_{2}}$
$R = {(w_{1}, w_{1}), (w_{1}, w_{2}), (w_{2}, w_{1}), (w_{2}, w_{2})}$
$D = {a, b}$
$I_{w_{1}} (F) = {a}$

$I_{w_{2}} (F) = \emptyset$

Here is a diagram for the model:

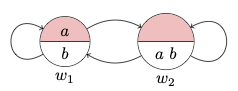
Now:

$M, w_{1} ⊮ \forall x (◻ F x \lor ◻ \neg F x)$ because $M, w_{1}, α [a / x] ⊮ ◻ F x \lor ◻ \neg F x$ . Yet:
$M, w_{1} ⊮ \forall x (◊ F x \land ◊ \neg F x)$ because $M, w_{1}, α [b / x] ⊮ ◊ F x \land ◊ \neg F x$ .

On the other hand, we may verify that constant domain models validate both the Barcan Formula and the Converse Barcan Formula.

Example 17.4 $⊨ ◊ \exists x F x \to \exists x ◊ F x$

Given a constant domain model $M$ and a world $w \in W$ such that $M, w ⊩ ◊ \exists x F x$ , let $u \in W$ be such that $R w u$ and $M, u ⊩ \exists x F x$ . That means that there is a member $d \in D$ such that for each assignment $α$ , $M, u, α [d / x] ⊩ F x$ . But then $M, w, α [d / x] ⊩ ◊ F x$ and, moreover, $M, w, α ⊩ \exists x ◊ F x$ . Since $α$ is arbitrary, $M, w ⊩ ◊ \exists x F x$ as required.

Example 17.5 $⊨ ◻ \forall x F x \to \forall x ◻ F x$

Given a constant domain model $M$ and a world $w \in W$ such that $M, w ⊩ ◻ \forall x F x$ , we argue that $M, w ⊩ \forall x ◻ F x$ . For given an assignment $α$ and a member $d \in D$ , $M, w, α [d / x] ⊩ ◻ F x$ . This is because given a world $u \in W$ such that $R w u$ , we have $M, u ⊩ \forall x F x$ and $M, u, α [d / x] ⊩ F x$ . Since $u$ and $d$ Are arbitrary, $M, w ⊩ \forall x ◻ F x$ as required.

Variable Domain Models

We have considered different strategies to weaken the simplest quantified modal logic, but we should now explain how to interpret the langauge in order to validate the framework that emerges.

Definition 17.7 (Variable Domain Model) We define a variable domain model to be structure $M$ of the form $(W, R, D, Q, I)$ , where:

$W$ is a non-empty set of worlds.
$R$ is a binary accessibility relation on $W$
$D$ is a non-empty set of individuals, which we will call the outer domain of the model
$Q$ is a function from $W$ into subsets of $D$ , and we will call $Q (w)$ the inner domain of $w$ for each $w \in W$
$I$ is a function from worlds $w$ into interpretations $I_{w}$ , which map each $n$ -place predicate $P^{n}$ into an $n$ -place relation over $D$ .

Definition 17.8 (Variable Assignment for a Model) A variable assignment $α$ for a model $M$ is a function from individual variables into members of $D$ .

The evaluation of an open formula such as $F x$ at a world $w$ in $W$ relative to an assignment $α$ raises an important question. What should we make of a case in which $α (x)$ is not in the inner domain of $w$ . Three broad strategies come to mind:

Avoidance

Find a way exclude such assignments in principle.
Unsettled Truth Value

Declare an open formula such as $F x$ to be neither true nor false in that circumstance.
Defer to the Interpretation Function

Defer to the interpretation function $I$ in order to settle the truth value of open formulas such as $F x$ .

In what follows, we will momentarily follow the third approach and let the interpretation function settle the truth value of the open formula at a world relative to that assignment. That means that a formula $F x$ can in principle be true at a world $w$ in a model $M$ relative to an assignment $α$ on which $α (x)$ is not even a member of $Q (w)$ .

Definition 17.9 (Truth at a World Relative to an Assignment) We use a recursive definition: $\begin{array}{lll} M, w, α ⊩ P^{n} v_{1} \dots v_{n} & if, and only if, & ⟨ α (v_{1}), \dots, α (v_{n}) ⟩ \in I_{w} (P^{n}) \\ M, w, α ⊩ v_{1} = v_{2} & if, and only if, & α (v_{1}) = α (v_{2}) \\ M, w, α ⊩ \neg φ & if, and only if, & M, w, α ⊮ φ \\ M, w, α ⊩ (φ \to ψ) & if, and only if, & M, w, α ⊮ φ or M, w, α ⊩ ψ \\ M, w, α ⊩ \forall x φ & if, and only if, & M, w, α [x / d] ⊩ φ for every d \in Q (w) \\ M, w, α ⊩ ◻ φ & if, and only if, & M, u, α ⊩ φ for every u \in W such that R w u \end{array}$

We now define truth at a world in a model and truth in. a model respectively:

Definition 17.10 (Truth at a World) A formula $φ$ is true at a world $w$ in a model $M$ , in symbols $M, w ⊩ φ$ , if, and only if, for all assignments $α$ for $M$ , $M, w, α ⊩ φ$

Definition 17.11 (Truth in a Model) A formula $φ$ is true in a model $M$ , in symbols, $M ⊩ φ$ , if, and only. if, for all $w \in W$ , $M, w ⊩ φ$ .

Definition 17.12 (Validity in a Class of Models) A formula $φ$ is valid with respect to a class $C$ . of constant domain models, in symbols $⊨_{C} φ$ , if, and only if, for every constant domain model $M \in C$ , $M ⊩ φ$ .

One important consequence of the choices we made above is that universal instantiation fails in variable domain models. Consider, for example, the evaluation of an instance of universal instantiation at a world $w$ of a variable domain model: $\forall x F x \to F y$ relative to an assignment $α$ , which maps $y$ to an individual that is neither in the inner domain of $w$ nor in the extension of $F$ in $w$ . We now set out to look at specific examples of variable domain models that falsify universal instantiation and the Barcan and Converse Barcan Formula.

Example 17.6 $⊭ ◻ \forall x F x \to \forall x ◻ F x$ .

Consider a variable domain model $M$ of the form $(W, R, D, Q, I)$ , where:

$W = {w_{1}, w_{2}}$
$R = {(w_{1}, w_{1}), (w_{1}, w_{2}), (w_{2}, w_{1}), (w_{2}, w_{2})}$
$D = {a, b}$
$Q (w_{1}) = {a}$
$Q (w_{2}) = {b}$
$I_{w_{1}} (F) = {a}$
$I_{w_{2}} (F) = {b}$

Now:

$M, w_{1} ⊩ ◻ \forall x F x$ .

This is because for every assignment $α$ for $M$ , we have both $M, w_{1}, α ⊩ \forall x F x$ and $M, w_{2}, α ⊩ \forall x F x$ .
$M, w_{1} ⊮ \forall x ◻ F x$

Given an assignment $α$ for which $α (x) = a$ , $M, w_{1}, α ⊮ ◻ F x$ , since $M, w_{2}, α ⊮ F x$ and $R w_{1} w_{2}$ .

Example 17.7 $⊭ \forall x ◻ F x \to ◻ \forall x F x$ .

Consider a variable domain model $M$ of the form $(W, R, D, Q, I)$ , where:

$W = {w_{1}, w_{2}}$
$R = {(w_{1}, w_{1}), (w_{1}, w_{2}), (w_{2}, w_{1}), (w_{2}, w_{2})}$
$D = {a, b}$
$Q (w_{1}) = {a}$
$Q (w_{2}) = {a, b}$
$I_{w_{1}} (F) = {a}$
$I_{w_{2}} (F) = {a}$

Now:

$M, w_{1} ⊩ \forall x ◻ F x$ .

This is because for every assignment $α$ for $M$ , for every $d \in Q (w_{1})$ , we have both $M, w_{1}, α [d / x] ⊩ F x$ and $M, w_{2}, α [d / x] ⊩ F x$ . In this case, $a$ is the sole member of the inner domain of $w_{1}$ .
$M, w_{1} ⊮ ◻ \forall x F x$

Given an assignment $α$ , $M, w_{1}, α ⊮ ◻ \forall F x$ , since $M, w_{2}, α ⊮ \forall x F x$ and $R w_{1} w_{2}$ .

The Inclusion and Converse Inclusion Requirement

Two broad constraints on variable domain models allow us to isolate the class of such models in which the Converse Barcan and the Barcan Formula are valid, respectively.

Definition 17.13 (Inclusion Requirement) A variable domain model $M$ of the form $(W, R, D, Q, I)$ satisfies the inclusion requirement if, and only if, for every $w, u \in W$ , if $R w u$ , then. $Q (w) \subseteq Q (u)$ .

Definition 17.14 (Converse Inclusion Requirement) A variable domain model $M$ of the form $(W, R, D, Q, I)$ satisfies the inclusion requirement if, and only if, for every $w, u \in W$ , if $R w u$ , then. $Q (u) \subseteq Q (w)$ .

That is, a variable domain model satisfies the inclusion requirement if the inner domains never decrease alongside the accessibility relation; and it satisfies the converse inclusion requirement if the inner domains never increase alongside the accessibility relation.

Proposition 17.1 The Converse Barcan Formula is valid in a variable domain models $M$ if $M$ satisfies the inclusion requirement.

Proof. Let $M$ be a variable domain model of the form $(W, R, D, I)$ satisfying the inclusion requirement. Choose a world $w \in W$ and an assignment $α$ for $M$ . We argue that $M, w, α ⊩ ◻ \forall x φ (x) \to \forall x ◻ φ (x)$ . Since the formula is a conditional, assume that $M, w, α ⊩ ◻ \forall x φ (x)$ . That means that $M, u, α ⊩ \forall x φ (x)$ for all $u \in W$ such that $R w u$ . We now argue that $M, w, α ⊩ \forall x ◻ φ (x)$ . That is that for every $d \in Q (w)$ , $M, w, α [d / x] ⊩ ◻ φ (x)$ . Pick a member $d \in Q (w)$ and let $u \in W$ be such that $R w u$ . Because $M$ satisfies the inclusion requirement, $d \in Q (u)$ . Since $M, u, α ⊩ \forall x φ (x)$ and $d \in Q (u)$ , $M, u, α [d / x] ⊩ φ (x)$ . We conclude that $M, w, α ⊩ ◻ \forall x φ (x) \to \forall x ◻ φ (x)$ And, more generally, $M, w ⊩ ◻ \forall x φ (x) \to \forall x ◻ φ (x)$

Proposition 17.2 The Barcan Formula is valid in a variable domain models $M$ if $M$ satisfies the converse inclusion requirement.

Proof. Let $M$ be a variable domain model of the form $(W, R, D, I)$ satisfying the converse inclusion requirement. Choose a world $w \in W$ and an assignment $α$ for $M$ . We argue that $M, w, α ⊩ \forall x ◻ φ (x) \to ◻ \forall x φ (x)$ . Since the formula is a conditional, assume that $M, w, α ⊩ \forall x ◻ φ (x)$ . That means that $M, u, α [d / x] ⊩ ◻ φ (x)$ for all $d \in Q (w)$ . We now argue that $M, w, α ⊩ ◻ \forall x φ (x)$ . That is that for every $u \in W$ such that $R w u$ , $M, u, α ⊩ \forall x φ (x)$ . Pick a word $u \in W$ such that $R w u$ and let $d \in Q (u)$ . Because $M$ satisfies the converse inclusion requirement, $d \in Q (w)$ . Since $M, w, α [d / x] ⊩ ◻ φ (x)$ and $M, u, α [d / x] ⊩ φ (x)$ . So, generalizing, $M, u, α ⊩ \forall x φ (x)$ and $M, w, α ⊩ ◻ \forall x φ (x)$ . We conclude that $M, w, α ⊩ \forall x ◻ φ (x) \to ◻ \forall x φ (x)$ And $M, w, α ⊩ \forall x ◻ φ (x) \to ◻ \forall x φ (x)$ .

Here are two more examples of validities in free quantified modal logic.

Example 17.8 $⊨ F x \to F x$

This formula is valid in every variable domain model $M$ of the form $(W, R, D, Q, I)$ because given a world $w \in W$ and an assignment $α$ , $M, w, α ⊩ F x \to F x$ , regardless of whether $α (x)$ is in $Q (w)$ or not.

Example 17.9 $⊨ ◻ \forall x F x \to \forall x ◻ (\exists y x = y \to F x)$

Let $M$ be a variable domain model of the form $(W, R, D, I)$ . Choose a world $w \in W$ and an assignment $α$ for $M$ . We argue that $M, w, α ⊩ ◻ \forall x F x \to \forall x ◻ (\exists y x = y \to F x)$ . Since the formula is a conditional, assume that $M, w, α ⊩ ◻ \forall x F x$ . That means that $M, u, α ⊩ \forall x F x$ for all $u \in W$ such that $R w u$ . We now argue that $M, w, α ⊩ \forall x ◻ (\exists y x = y \to F x)$ . That is, for every $d \in Q (w)$ , $M, w, α [d / x] ⊩ ◻ (\exists y x = y \to F x)$ . Pick a member $d \in Q (w)$ and let $u \in W$ be such that $R w u$ . There are two cases. If $d \notin Q (u)$ , then $M, u, α [d / x] ⊮ \exists y x = y$ and $M, u, α [d / x] ⊩ \exists y x = y \to F x$ . Otherwise, if $d \in Q (u)$ , then since $M, u, α ⊩ \forall x F x$ and $d \in Q (u)$ , $M, u, α [d / x] ⊩ F x$ and $M, u, α [d / x] ⊩ \exists y x = y \to F x$ . Either way, $M, u, α [d / x] ⊩ \exists y x = y \to F x$ , and $M, w, α ⊩ ◻ (\exists y x = y \to F x)$ . We conclude that $M, w, α ⊩ ◻ \forall x F x \to \forall x ◻ (\exists y x = y \to F x)$ And, more generally, $M, w ⊩ ◻ \forall x F x \to \forall x ◻ (\exists y x = y \to F x)$ .